November | 2009 | Not About Apples

The Galois Correspondence

30 November 2009

Lately we’ve been talking about fields, which are structures made of numbers, and groups, which are structures made of symmetries; we recently established a connection between the two in the form of Galois groups. To see the full beauty of the theory, we need to add one last layer of complexity. Today we will look at so-called intermediate fields; we will see there is a close relationship between the arrangement of intermediate fields and the structure of the Galois group.

An Example

Consider the field $\mathbb{Q}(\sqrt{2},\sqrt{3})$ , which is obtained by starting from the rational numbers and attaching the square roots of 2 and 3. It turns out this is just the set of numbers of the shape $a+b\sqrt{2}+c\sqrt{3}+d\sqrt{6}$ , where $a,b,c,d$ are fractions. (It might not be totally obvious that this thing is a field, but it is.) We’ll be thinking of this as an extension of the smaller (and more familiar) field of fractions $\mathbb{Q}$ .

Read the rest of this entry »

Leave a Comment » | Articles | Tagged: galois correspondence, Galois theory | Permalink
Posted by Cap Khoury

Quotations: A Baker’s Dozen

24 November 2009

This semester I have taken to the habit of writing a quote of the day on the board for my Geometry for Teachers class. When possible, I choose a quote germane to the lecture topic, but a good number of them refer to mathematics more broadly. As I’ve looked though my notebooks, my favorite texts, and my memory for my favorite quotes, the ones that have helped me define for myself what mathematics means and why it is beautiful, it’s occurred to me that some of these bear mention here.

“If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.” — John von Neumann
“Do you know why the sun doesn’t revolve around the Earth? Because the idea is not beautiful enough.” — Einstein, in Steve Martin‘s Picasso at the Lapin Agile
“A mathematician is a device for turning coffee into theorems.” — Alfréd Rényi (but often misattributed to his friend Paul Erdös)
“Everything should be made as simple as possible. But no simpler.” — Albert Einstein
“Pure mathematics, may it never be any use to anyone.” — Henry J. S. Smith (a toast)
“Perhaps the most surprising thing about mathematics is that it is so surprising. The rules which we make up at the beginning seem ordinary and inevitable, but it is impossible to forsee their consequences.” — E. C. Titchmarsh
“It is one of man’s curious idiosyncracies to create difficulties for the pleasure of resolving them.” — Joseph de Maistre
“Practical application is found by not looking for it, and one can say that the whole progress of civilization rests on that principle. . . . ” — Jacques Hadamard
“The trouble with integers is that we have examined only the very small ones. Maybe all the exciting stuff happens at really big numbers, ones we can’t even begin to think about in any very definite way. Our brains have evolved to get us out of the rain, find where the berries are, and keep us from getting killed. Our brains did not evolve to help us grasp really large numbers or to look at things in a hundred thousand dimensions.” — Ronald Graham
“The art of doing mathematics consists in finding that special case which contains all the germs of generality.” — David Hilbert
“We often hear that mathematics consists mainly of ‘proving theorems’. Is a writer’s job mainly that of ‘writing sentences’?” Gian-Carlo Rota
“The mathematical sciences particularly exhibit order, symmetry, and limitation; and these are the greatest forms of the beautiful.” — Aristotle
“As for everything else, so for a mathematical theory: beauty can be perceived but not explained.” — Arthur Cayley

P.S.

Somehow I managed to publish an incomplete version of the previous post, several drafts back. If you read this post and thought I might have lost my marbles, the correct version of the post is there now.

Leave a Comment » | Articles | Tagged: quotes | Permalink
Posted by Cap Khoury

Symmetries of Number Systems

19 November 2009

I know it’s been a long time since my last Galois Theory post; my apologies.

When last we met, we had introduced two important algebraic structures: the group and the field. At least superficially these are similar mathematical concepts, in that both are sets of things with operations that satsify certain rules, but we aren’t thinking of them the same way. We think of the objects in a group as symmetries (and the operation is function composition); we think of the objects in a field as numbers (and the operations as addition and multiplication). (See the last two posts for a refresher, or else see the corresponding wikipedia articles for an overflow of information.)

What’s missing in this story is the interaction between these structures. That is, what are symmetries of a number system? The answer is easy to state: a symmetry is any permutation of the numbers in the field which preserves addition and multiplication. That is, it is a function $\phi$ from $F$ to $F$ such that $\phi(x+y)=\phi(x)+\phi(y)$ and $\phi(xy)=\phi(x)\phi(y)$ . Saying that the symmetry preserves the basic operations is the same as saying that the symmetry preserves any possible statement in the language of basic algebra. These symmetries have a fancy name: field automorphisms.

Whenever you have a symmetry, it’s interesting to think about about which objects correspond to themselves under the symmetry. In geometric contexts, you already know this: when you think of a reflection, you think first of the axis of reflection, and when you think of a rotation, you think first of the point about which you are rotating. And any symmetry of a field has to leave certain numbers alone. If $\phi$ is an automorphism of any field, we must have $\phi(0)=0$ , because $0+0=0$ , so $\phi(0)+\phi(0)=\phi(0)$ and no other number is like that. Likewise, $\phi(1)=1$ , and then we have $\phi(p/q)=p/q$ for any rational number $p/q$ . That is, every symmetry of every field has to fix the rational numbers.

Remarks on the Definition

Am automorphism of any algebraic structure—a group, a field, a ring, a module, etc.—is just a permutation of its elements which preserves the structure. So a group automorphism is a permutation of the group elements which preserves group composition. (So symmetry groups have their own symmetry groups…wild.)
Actually, automorphism groups are themselves a special case of a more general template for constructing interesting groups. If you have a configuration of objects, the collection of all the permutations of the objects which preserve some interesting properties is automatically a group in a natural way.
Every symmetry must fix the rational numbers, at least; that is, a symmetry might happen to leave even more numbers alone. This, it will turn out, is where things really get interesting.
I’m implicitly assuming that the field we’re talking about has a copy of $\mathbb{Q}$ inside it. This is true about most fields that you probably care about; more precisely it is true for any field where repeatedly adding up 1’s does not ever give 0. In more exotic cases, so-called fields of positive characteristic, the role of $\mathbb{Q}$ is played by some other simple field. For ease of language, I’ll gloss over this point.
Symmetries preserve rational numbers because they can be expressed in terms of the basic operations and 0 and 1, and 0 and 1 can themselves be completely described in terms of the operations. This should remind you of the alien posts; essentially this is the reason why it’s always straightforward to establish shared language for the rational numbers.

Now, it might happen that we want to insist that an automorphism of a field $E$ fix some smaller field $F$ . In the first alien post, we were able to establish the real number system by bringing in some other concepts, so the only symmetries of the complex numbers that made sense in context were the ones that preserve the real numbers. We call this the symmetry group of $E$ relative to $F$ .

The group of symmetries of a field $E$ relative to a subfield $F$ is called the Galois group $G(E/F)$ . (The slash is read as “over”, not “divided by”.) If you don’t operate relative to some subfield (which really just means you are operating over the prime field), that’s called the absolute Galois group $G(E)$ or $G(E/\mathbb{Q})$ .

There is a direct connection between the Galois group and the alien thought experiment. If two parties have possibly different languages for talking about the field $E$ , but they know they agree on the smaller field $F$ , then each element of the Galois group $G(E/F)$ corresponds to a way of matching up their vocabularies for $E$ compatibly with $F$ .

In some sense, then, the larger the Galois group is, the more complicated the extension is. But we can be a great deal more explicit than this. In the next installment we’ll see that, under the right circumstances, there is a very precise correspondence (the so-called Fundamental Theorem of Galois Theory) between the structure of the Galois group and the structure of a field extension.

Leave a Comment » | Articles | Tagged: automorphism, field, galois group, Galois theory, symmetry | Permalink
Posted by Cap Khoury

Borderlines

7 November 2009

This is another digression from the Galois theory arc (and Joe, I don’t know if you read the Not About Apples stuff, but you are definitely to blame for the fact that I call it an arc) inspired by a recent conversation with one of my students in my geometry for teachers class.

A major topic of the class is an exploration of some famous attempts in history to prove Euclid’s Fifth Postulate and what we can learn from how they went wrong. Among the proofs considered is one due to the French mathematician Gergonne (a name probably best known for the “Gergonne point” in triangle geometry). In a nutshell, he argued that since there’s no single largest acute angle that can appear in a right triangle, every acute angle can appear in a right triangle. That’s all you really have to know, since geometry really isn’t what I came here to talk about, so much as a resulting conversation from office hours yesterday.

It turns out the flaw in his reasoning is interesting, and it’s something you’ve probably never given a lot of thought to. And it has nothing to do with geometry. Imagine that, in some context, numbers that are small enough are “good” and numbers that are big enough are “bad” (that is, if a number is good, all smaller numbers are also good, and if a number is bad, all bigger numbers are also bad). The idea underlying Gergonne’s mistake is that if there are good numbers and bad numbers, then there must be a single largest good number “at the borderline”. But this is not so. Is there a largest negative number? No. Zero is the best upper bound to the negative numbers (the so-called supremum), but zero isn’t a negative number. Whatever negative number you can think of, there is another negative number closer to zero. Likewise there is no smallest positive number.

What is true is that, if there are good numbers and bad numbers, then there is either a single largest good number or a single smallest bad number, Never neither, never both. In particular, just because a set of numbers doesn’t actually have a maximum doesn’t mean it isn’t bounded; it could just be that the boundary point isn’t the set.

So why is this counterintuitive? Because most people so often think about integers, and integers are not like that. Integers are spaced differently on a number line than real numbers; the technical term is discrete. If you have good integers and bad integers, then it much be that there is a largest good number and a smallest bad number.

This relates to the fact that the counting numbers are well-ordered. In other words, in any nonempty set of counting numbers, there is always a single smallest number. This is the foundational idea for a powerful technique for proving mathematical theorems and grappling with the infinite, so called mathematical induction. But that’s another story. For another time.

Now you might think we’ve said all there is to say. We’ve described the behavior of real numbers (a continuous set) and the behavior (a discrete set), and you might not think any other behaviors would be possible. But rational numbers behave in an even more unexpected way. If you divide a range of fractions into small/good ones and large/bad ones, then there are three possible behaviors.

there is a largest good number, but no smallest bad number
there is a smallest bad number, but no largest good number
there is neither

The last case may be hard to picture. Here is an example. Let’s look at just the positive fractions, and call a number $x$ good if $x^2<19$ and bad if $x^2>19$ . Then there is no largest good number and no smallest bad! The “borderline” in this case appears to be $\sqrt{19}$ , but that’s not a rational number! There’s a hole in the number line where the boundary should be!

Leave a Comment » | Articles | Tagged: Dedekind cut, induction, infimum, maximum, minimum, supremum | Permalink
Posted by Cap Khoury

Number Systems

5 November 2009

People mean different things by “number” at different times. Sometimes “numbers” means integers, or counting numbers, or real numbers, or fractions, complex numbers, or maybe something else entirely. There are a wide variety of number systems that we might use in various contexts. Today I will describe fields, a certain kind of algebraic structure which expresses exactly what I mean by “number system” for the purposes of Galois theory.

For those of you still reeling from the definition of a group, don’t worry. A field is a much easier thing to get your head around. It’s just a collection of things (I’ll tend to call the things in a field “numbers”) where we have the four basic operations (addition, subtraction, multiplication, and division by anything but zero) and the operations behave the way you’re used to.

What do I mean by “the way you’re used to”? I mean the following.

addition is commutative ( $a+b=b+a$ )
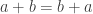addition is associative ( $a+(b+c)=(a+b)+c$ )
0 is the additive identity ( $a=0+a$ )
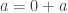subtraction is the “opposite of addition” in the sense that $a + (b-a) = b$
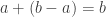
multiplication is commutative ( $ab=ba$ )
multiplication is associative ( $a(bc)=(ab)c$ )
1 is the multiplicative identity ( $a=1a$ )
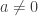division is the “opposite of multiplication” in the sense that $a (b/a) = b$ , assuming $a\neq 0$ .
multiplication distributes over addition ( $a(b+c)=ab+ac$ )

To use the lingo of group theory, we are saying that the elements a field form a commutative group under addition, that the elements (except 0) form a commutative group under multiplication, and that the two operations are related by the distributive law. But if that’s confusing, forget what I just said.

Digression. When I was a child, I wondered why mathematicians could invent imaginary numbers so that we could take square roots of negative numbers, but no one ever tried to similarly finesse division by zero by making up a new number to play the role of 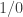$1/0$ . Why not? Why was division by zero so much harder than square roots of negative numbers. 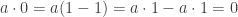Notice by the way that, if any $a$ is any number whatsoever in any conceivable field, then the distributive law $a\cdot 0= a(1-1)=a\cdot 1 - a\cdot 1 = 0$ . That is, the common notion that anything times zero is zero is fully universal. It’s not just a statement about real numbers, it’s a statement about what it means to be a number. That’s the difference. No real number squared is negative, but that’s an obstacle specific to the real number line. No number of any kind, in any context we would recognize, times zero is one.

You already know about several important fields. Here are some examples

$\mathbb{Q}$ , the field of all rational numbers
$\mathbb{R}$ , the field of all rational numbers
$\mathbb{C}$ , the field of all complex numbers
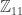$\mathbb{Z}_{11}$ , the field of integers modulo 11 (convince yourself that division really works here!)
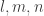$\mathbb{Q}(i)$ , the field of all complex numbers $\frac{l+mi}{n}$ ( $l,m,n$ integers) for which both the real and imaginary part happen to be rational numbers (again, it is not totally obvious that division works out right; the key is rationalizing the denominator, like Mrs. Gunderson taught you in school)

There are also some important nonexamples. In some other contexts, these may be called number systems, but they are not fields, the kind we care about now.

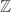$\mathbb{Z}$ , the integers
$\mathbb{Z}_{12}$ , the integers taken modulo 12 (why is this different than modulo 11?)

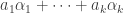A particularly interesting situation occurs when one field contains another, as the complex numbers contain the real numbers. Note that every complex number has an expression in the form $a+ib$ , where $a,b$ are real. Whenever there is a finite list of elements $\{\alpha_1,\alpha_2,\ldots,\alpha_k\}$ and every element in the larger field has a unique expression in the form $a_1\alpha_1+\cdots+a_k\alpha_k$ , we say that the larger field is a finite extension, and $k$ is the degree of the extension. So the complex numbers are a degree-2 extension of the real numbers (and the natural basis is $\{1,i\}$ ).

The usual way to manufacture finite extension fields is to begin with a field and some polynomial that does not have solutions in the field, and then enlarge the field just enough so that the polynomial can be solved. This is how 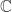$\mathbb{C}$ arises, by beginning with $\mathbb{R}$ and adding solutions to $x^2+1=0$ . This will always produce a finite extension field. In fact, it turns out that in some sense this is the only way to get finite extensions. That is, if $E$ is a finite extension of $F$ , then there is some polynomial $p(x)=0$ over $F$ such that $E$ is obtained by adding a root of $p(x)=0$ to $F$ .

Finite extensions of 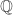$\mathbb{Q}$ have a special role in mathematics; they are called (algebraic) number fields.

(Most of what I just said is intuitively plausible, though some of it may be surprising. Almost none of it is obvious, but proofs can be found in any introductory algebraic number theory text for those who want.)

I have said that Galois theory is about the symmetries of number systems. If $F$ is a field and $E$ is some field containing $F$ , then we will want to study the symmetries of $E$ over $F$ ?

So what, exactly, is the right thing to mean by a symmetry of a number system? In the case of 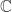$\mathbb{C}$ over $\mathbb{R}$ , it was somehow clear that the right things to consider were complex conjugation and the trivial symmetry. But more generally, what is a symmetry of one number system relative to another? And what can we learn by understanding them?

I’ll tell you next time, Gadget.

Leave a Comment » | Articles | Tagged: division by zero, extension field, field, Galois theory, number theory | Permalink
Posted by Cap Khoury

Increasing vs. Unbounded

4 November 2009

This post is pure digression from the Galois theory arc, but I think it’s worth making. There are some fundamental confusions which seem to be endemic among non-mathematicians. I was reminded of this one as part of the geometry course I am teaching, in a discussion of Aristotle’s axiom. I thought to myself then that this conflation of ideas had nothing to do with geometry, was much more primitive than that, and I was surprised by how hard I had to work to get my students to see the light.

The problem, I think, is one of language. The imprecision of language because imprecision of thought. In this case, the key phrase is “bigger and bigger and bigger”. Suppose there is some quantity which changes over time, and someone says it gets bigger and bigger and bigger. What would that mean? There are two primary interpretations.

the quantity is larger each moment than it was in the past; i.e., the quantity is increasing.
the quantity will eventually get larger than 1000, larger than 1000000, larger than any quantity you can name; i.e., the quantity is unbounded.

Well, you might think that these are pretty much the same thing. If something is always increasing, won’t it have to eventually be huge? The answer is an emphatic no.

Consider the following graph of the function $y=f(x)=\frac{e^x-1}{e^x+1}$ (made on wolframalpha). As you move the right, the graph gets higher and higher. This function is increasing. But it never reaches its asymptote at $y=1$ , and it certain never achieves values as large as 1000.

graph1 Perhaps you find this unpersuasive, because I gave you a graph and a formula. Perhaps you feel that I’m cheating by resorting to esoteric mathematical stuff.

So I will tell you a story, the story I told my class which made the penny drop. Imagine a person, my personal grader, with a very simple life. Each day my grader gets up, picks up the stack of grading for the day, grades it until it’s done, and then plays video games until the day ends. Every day he gets the same amount of grading to do, and it’s always the same monotonous task. The first day he doesn’t finish until 7 p.m., and he gets 5 hours of video games. But the grader gets better and better at grading, a little more efficient every day. So each day he finishes a bit sooner. Then his daily video game time is “getting bigger and bigger” in the sense that it is increasing. If you really believe that increasing implies unbounded, then you must also believe that, eventually, he’ll be playing video games for hundreds of hours, hundreds of years, hundreds of centuries, every day.

Leave a Comment » | Articles | Tagged: common misunderstanding, increasing, unbounded | Permalink
Posted by Cap Khoury