Mathematician-Speak: Impossible

When I was in college, I spent a lot of time with a certain science major who just couldn’t seem to get the Zen of mathematics.  Whenever I would say something like “there is no formula for the roots of a fifth-degree polynomial”, she would reflexively correct “You mean, there’s no formula you know about.”

But no, I really mean that there is no formula.  I mean it is impossible to find such a formula.  And when a mathematician doesn’t say “impossible” lightly; it doesn’t mean “no one’s ever done it” or “it’s prohibitively hard” or “it seems hopeless”.  It means impossible.

It might seem hard to believe that people can ever know things are impossible.  How is mathematical impossibility different from garden-variety closed-mindedness?

But there is more going on here than “I’ve seen a lot of things, and if never seen something like [X], then [X] doesn’t exist.”  There’s a lot more.  In fact, often one can learn a lot more from proving a problem has no solution than from solving a problem.

Multinomial Coefficients and Farkle

This is the first in a series of planned articles about Farkle and its strategy.  Lately, I’ve been spending alittle too much time playing Farkle on Facebook. In case you’re not familiar, Farkle is a dice game. It used to be pretty well-known before becoming overshadowed by the popularity of its distant cousin Yahtzee.

Like all the old games, there are a certain number of variations, but the Facebook version is pretty mainstream. For the purposes of this article, we’ll use that version of the rules.

The goal is to gain points by rolling scoring combinations with dice. The scoring combinations are as follows: three (or more) of a kind, 1’s and 5’s, three pairs, and a 1-2-3-4-5-6 straight. (For today’s purposes we don’t care how much the various scoring combinations are worth, only what they are.) You start with six dice. After each roll, you set aside one or more scoring combinations (you must score at least some dice after each roll). Then you can either roll the remaining dice, hoping for more points, or save your points and end the turn.  If you use up all six dice in scoring combinations, you get a new set of six dice.  But if ever you roll and you don’t get any scoring combinations, you “farkle out” and lose all the points you’ve scored this turn. (This is a bad thing.)

Today we’ll start with a fundamental question: if I roll a certain number of dice, how likely am I to farkle out?

Casting Out Nines (and Elevens and Sevens . . .)

Most of you probably know (or knew at one time) the trick from pre-calculator days for deciding quickly whether a number is divisible by 9. You add up all the digits, and if the result is divisible by 9, then so was the original number. If you like, you can repeat the process, just summing the digits until only a one-digit number remains; if you started with a multiple of 9, the number you get will be a 9; otherwise, it won’t. I’ve heard that this process is well-known to numerologists under the name “casting out nines”.

What you may not know is that the same rule tests for divisibility by 3, and that a very similar rule tests for divisibility by 11.

Direct Digit Casting for 3 and 9: Start with a number. Add up the digits to get a new number. (Repeat as desired.) The original number is divisible by 3 (or 9) if and only if the new number is divisible by 3 (or 9).

Alternate Digit Casting for 11: Start with a number. Working from right to left, alternately add and subtract the digits. (Repeat as desired.) The original number is divisible by 11 if and only if the new number is divisible by 11.

Examples:

is divisible by 9 because is divisible by 9.

is divisible by 3 but not by 9, because is divisible by 3 but not by 9.

is not divisible by 3, because is not divisible by 3.

is divisible by 11 because is divisible by 11.

is not divisible by 11 because is not divisible by 11.

So what is going on? Why does this work? Are there other rules like this?

Most of you probably know (or knew at one time) the trick from pre-calculator days for deciding quickly whether a number is divisible by 9. You add up all the digits, and if the result is divisible by 9, then so was the original number. If you like, you can repeat the process, just summing the digits until only a one-digit number remains; if you started with a multiple of 9, the number you get will be a 9; otherwise, it won’t. I’ve heard that this process is well-known to numerologists under the name “casting out nines”.

What you may not know is that the same rule tests for divisibility by 3, and that a very similar rule tests for divisibility by 11.

Direct Digit Casting for 3 and 9: Start with a number. Add up the digits to get a new number. (Repeat as desired.) The original number is divisible by 3 (or 9) if and only if the new number is divisible by 3 (or 9).

Alternate Digit Casting for 11: Start with a number. Working from right to left, alternately add and subtract the digits. (Repeat as desired.) The original number is divisible by 11 if and only if the new number is divisible by 11.

Examples

• is divisible by 9 because is divisible by 9.
• is divisible by 3 but not by 9, because is divisible by 3 but not by 9.
• is not divisible by 3, because is not divisible by 3.
• is divisible by 11 because is divisible by 11.
• is not divisible by 11 because is not divisible by 11.

So what is going on? Why does this work? Are there other rules like this?

The Pythagorean Theorem and the Square Root of 2

Most of you probably remember the Pythagorean Theorem, and the rest of you probably remember that there was a time when you remembered it. The Pythagorean Theorem relates the lengths of the sides of a right triangle. If and are the lengths of the shorter sides (the legs) of a right triangle and is the length of the longest side (the hypotenuse), then .

In other words, if you draw three squares based on the side lengths of the triangle, the total area of the smaller two is equal to the area of the largest.

The Pythagorean Theorem is named for Pythagoras, a Greek mathematician. To be fair, he was not the only person to do so. This fact, so fundamental to geometry and measurement, was known independently to many ancient cultures, and in some places there is evidence that the fact was known long before Pythagoras.  I like to think that the theorem bears Pythagoras’ name because he is the most colorful choice for a namesake — mathematician, numerologist, leader of a secret society (yes, really!).

What you might not expect is that it is actually quite simple to see why the Pythagorean Theorem is true. You don’t have to be an ancient mathematician shrouded in mystery to discover it.  Actually all it takes is some paper squares cut into colored pieces.

(How this illustrates the Pythagorean Theorem is explained after the jump . . . but try to see it for yourself before reading on.)

Counting to Infinity (Part II)

In the previous article in the series, we looked at what it means for a set to be infinite. We mostly looked at countable sets, sets whose elements can be “listed”. This time we set our sights higher, and look at even bigger sets, the uncountable sets that have too many elements to list.

Bounded Intervals

We have seen one uncountable set so far — the set of all real numbers between o and 1, usually written . The set of all real numbers is usually written .  We know is uncountable, since it contains the interval , but it is the same size? In other words there are at least as many real numbers as there real numbers between 0 and 1, but it is true that there are more real numbers than real numbers between 0 and 1?

We’ll start with an easier question. The notation means the interval of all real numbers that are at least and at most .

Can we compare the intervals and ? Geometrically, these are line segments on the number line; the former has length 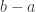and the latter has length 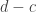. If one of the lines is much longer, we might expect it to be larger as a set.

However, the relation gives abijection between points in the interval and points the interval .  (Don’t be intimidated by the algebra notation — the correspondence just matches the left endpoint of one interval to the left interval of the other and rescales so that the right endpoints match up.)

So every interval is the same size (in the set -counting sense), no matter how long it is. (Geometric length and set size are fundamentally different ways of measuring.)

Then it’s probably not unexpected that it doesn’t matter whether or not we include the endpoints of the various intervals involved.  So all the different types of bounded intervals.

are the same size as sets, no matter what numbers are used.

Lines and Squares

Now lets try to find a set that really is larger than an interval. Lines are one-dimensional, so a good guess is something two-dimensional. How does the number of points in a line segment compare to the number of points in a square.

The points on a square can be represented by pairs of numbers in a certain range. So it will be enough to know the following (counter-intuitive) fact.

Theorem. The set of all numbers is the same size as the set of  pairs of numbers .

Proof. Starting with a number , write it is a decimal expansion 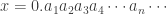. If has two decimal expansions, use the one that ends in all zeroes, not the one that ends in all nines.  Then cluster the digits so that each 9 or group of 9s is attached to the following digit.  So, if a number began

,

I would think of it as

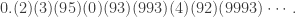
Then form a pair of numbers by taking alternate clusters. Hard to verbalize, easy to do:

This associates to each number in the range a pair of numbers in the range. It turns out that every pair of numbers shows up in this way exactly once. This is a one-to-one correspondence.

If you’re wondering why I do that strange trick with the clustering digits instead of just alternating digits, it has to do with avoiding that technicality I mentioned in the previous article, so that numbers with two decimal expansions still only show up once.

We can repeat this trick to see that line segements, squares, and cubes are all the same size as sets. Since we know that a bounded line segment has the same number of points as , it’s probably not any more surprising that it already was when I tell you that an entire plane and all of three-dimensional space each has the same number of points as .

But wait a minute. It seems intuitively clear that a line segment and a square are not the same size. You could “stack” millions and millions and millions of line segments inside a square without making any progress toward filling the square up. Put another way, a square has an area. A square which is 1 unit on a side has area 1, while a line segment which is 1 unit long has area 0. How can we reconcile this with what we just said? Stay tuned, friends…we will answer this question in a future article.

…and beyond. Way beyond.

So far we have found infinite sets of two different sizes.  We have all the countably infinite sets, as well as the set of real numbers (or equivalently the set of points in a line segment or square), which is larger. Are there more possible sizes? Can we list all the possible sizes of sets? Is there a largest infinite number (because if there is, it’s sets of that size we should really call infinite)?

Questions like this get deep and philosophical in a hurry, so for now I’ll settle for showing you why there is no largest infinite set.

This theorem is due to Georg Cantor, who is in fact responsible for all the essential concepts in this article. My style of presentation is no doubt influenced by many writers, not least of whom is Raymond Smullyan. A very clever alternate presentation can be found in the outstanding book The Heart of Mathematics by Berger and Starbird.

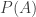To progress, we need the notion of the power set. If is any set, then is the collection of all the subsets of . So if , then . In this case the original set has 3 elements while its power set has 8.

Theorem. No matter what set is, 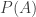is a strictly larger set.

This is pretty obvious for finite sets. If a set has elements, it’s not hard to show that its power set has 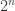(think about why). This is “yardstick” thinking, though, and it won’t do us much out here in the realms of infinity. Remember that the set of pairs of integers was no bigger than the set of integers. So intuition can be misleading.  But here is a reason.

Proof. Let be any set, and consider its power set 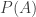. It should be apparent that is not bigger than its power set (but think about why if it is not clear). So the only issue is whether it is possible that there could be a bijection between a set and its power set.

Suppose that is a set which can be placed in a one-to-one correspondence with 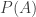. Then we can take every subset of and label it with an element of . Every element is used as a label once and once only, and every subset of is labelled. Now, for an particular element of , it may belong to the subset it labels, or then again it may not. Call an element of good if it so happens to belong to the set it labels, and bad otherwise. Then we can split up into two pieces — , the set of good elements, and , the set of bad elements.

We know that has a label, which we shall call . Now can’t be good, because if it were, it would have to be in the set it labels, , but only bad elements are in there.  Likewise cannot be bad — if it were bad it would belong to , and since it belongs to the set it labels, it cannot be bad.  This is impossible.

The conclusion is that cannot possibly be put in one-to-one correspondence with .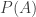

In particular, there are more sets of integers than there are integers. It turns out, actually, that there are the same number of sets of integers as there are real numbers.

So there is no such thing as an “ultimate” infinity. Given any set we can describe, however incomprehensibly huge, we can describe another set which is strictly bigger. If we start with any infinite set (such as the smallest infinite set, 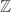), we can build a tower of progressively larger infinite sets.

Counting to Infinity (Part I)

People have always had a great curiosity about the infinite. I think this is because infinity represents a palpable break between our mind and our experience. You probably don’t have much difficulty imagining an infinite row of apples, but you’ve never seen one and you never will. Among the religious and spiritual, it is not unusual to identify the infinite with the divine. A great triumph of mathematical thinking, I feel, is the fact that it enables us to actually talk meaningfully about infinite things.

When people find out that I am at a mathematician, sometimes they will ask me questions. This is very interesting for me, because I get some insight into what sort of mathematical things nonmathematicians think about. A large percentage of those questions involve infinity in some way. Two popular ones are ‘Can you count to infinity?” or “Are there different kinds of infinity?” The former question strikes me as rather Zen, hence its inclusion as the title of this article. Today we’ll give at least one answer to the latter question.

How many prime numbers are there?

“You can’t deal with my infinite nature.”

“That is so not true.  Wait, what does that even mean?”

— I Heart Huckabees

So far, this blog has dealt with questions that are nontrivial to formulate but easy to answer.  Today I want to talk about a question about prime numbers which is not at all easy to answer.  Indeed, in many ways this is the starting point for the branch of mathematics where I live, number theory.

In number theory, we are especially interested in prime numbers.  (Quick and dirty definition in case it’s been a while: a prime number is an integer greater than 1 which cannot be written as a product of two integers greater than 1.)  The first few prime numbers are pretty easy to find just by trial and error.

So how many of these things are there?  Could we keep making this list as long as we want, or would we eventually run out of prime numbers?  In other words, which of the following alternatives is true?

Alternative A: There are infinitely many primes.  (There is no largest prime.)

Alternative B: There are only finitely many primes.  (There is a largest prime.)

I claim I know which of these statements is true and which is false.  I don’t just mean I have a persuasive guess, I mean I know.  One of those statements is right and one is wrong and there is no room for confusion about which is which.  Actually, this is a fundamental fact which should be known by any math major at any college in the world.

Notwithstanding what I just said, think about how preposterous it is to try to answer this question.  How could you ever know either of these things?  If you believe alternative A, then you have to believe that no matter how many prime numbers I have written down, you could find one larger than any of them.  If you believe alternative B, then you have to believe that there is a finite list of prime numbers, and no matter what number I say, however gigantic, all its prime factors are on the list.  Either way, we are claiming to know an infinite number of pieces of information.

You could get the faster supercomputer in the world to hunt for primes, but that wouldn’t help in the least.  No matter how many billion primes it found, that would be no guarantee there would be any more.  No matter how may years it went without finding another prime, that would be no guarantee it wouldn’t find one tomorrow.  So computational brute force is no good here.

It seems like a fool’s dream to want to settle the matter once and for all.  Nonetheless, we’ll answer it together after the cut.

Think about which alternative you’re leaning toward before reading further.

Zero Factorial

Those of you have taken math classes in high school probably learned about factorials, which are written with “” symbols.  The usual definition is something like the following.

Definition. For a positive integer n, we define (read: n factorial) as the product of all the positive integers up to and including .

and so forth.

The factorials can be defined by the fact that is the number  of ways to put objects in order.  They are ubiquitous in combinatorics (read: counting) and also show up in lots of other sorts of equations and formulas.  Sooner or later, it comes up that mathematicians don’t just use factorials of positive integers, and shows up on the chalkboard.  Then the questions start.  Because almost all students expect   to be zero.  And the exasperated teacher says something like the following.

“Okay, zero factorial is one.  It just is.  There’s doesn’t have to be a reason, there’s nothing to try to understand, it’s just a mathematical convention.  .”

But there are good reasons to decide that , not just to take some teacher’s word for it but to know that it’s the right thing.  And I have more faith in you, fair reader, than your math teacher did.  I believe that anyone who wants to understand it can.

If you keep reading, you’ll find three ways of getting at zero factorial, including shrieks, a math koan, and the nature of nothing.

Mathematician-speak: Modulo

Being a mathematician who spends much of his time talking to nonmathematicians, I find I often have to censor myself, because the way I want to say something uses mathematical jargon.  Times when I forget to censor myself are often mistaken for trying to make myself seem more confusing or complicated.  Actually, it’s just the opposite — mathematicians have lots of words and constructions to deal very precisely with complex ideas, and it’s not unusual for them to be useful in “real life” too.

Hence the first in a series of short and potentially useful posts.  Whether you want to understand a mathematician better or to try to pass yourself off as one at a cocktail party, I’m here to help.

Today’s word: modulo.

A is for abstraction

At the heart of mathematical thinking, as I see it, is the notion of abstraction.  It is unfortunate that this word seems to be a turn-off for so many people.  I often hear people say that they liked math until it got “too abstract”.  I think statements like that come from a faulty analogy with other senses of the word “abstract”.  In the art world, for example, there is a distinction between the representational and the abstract, and so it is tempting to think of “abstraction” as the opposite of “concreteness” or “reality”.  From there it’s a short step to thinking of “abstraction” as the opposite of “relevance” or “importance”.

But I think this misses the point and misses it rather dramatically.  So just for today, I would like you to forget the adjective “abstract” and focus instead on the verb “abstract”.  I’m not talking today about abstract-ness, I’m talking about abstract-ing, an action word, about what it means to abstract a concept from a situation.  I realize that the verb doesn’t get much use in general discourse, but bear with me.  The reason we don’t use it much is many of us haven’t done much conscious, serious, powerful abstracting since we were very small.

So I’m not going to bury you in high-level, complicated mathematics today.  Actually, I’m going to do just the opposite.  I want you to think very, very hard about something really, really simple, something you probably haven’t given much real attention to in a long time.  That something is the addition of whole numbers.

That’s right, this is an article about 1 + 2 = 3.  Because believe it or not, 1 + 2 = 3 is a spectacularly deep mathematical discovery.  Really!

Imagine yourself in the distant history of the human race.  Perhaps you live in a cave, or some sort of hut.  You have some words, but not a lot.  You certainly don’t have math classes.  And you’re about to become the world’s first mathematician, because you are thinking very hard about the apple on the giant rock that serves as your table, a short distance from two more apples, and you are about to have great insight.  And the insight is not “one apple plus two apples is three apples” (or, as you would more likely verbalize it “apple and apple-apple are apple-apple-apple”).  That’s easy.  That’s obvious.  That’s not mathematics.  The heart of mathematics is realizing that “one apple plus two apples is three apples” is not about apples.